warp-CTC
Shing-Yun Jung 20180324
Connectionist temporal classification(CTC) is a probabilitistic model usually used as the loss function for RNN-based speech recognition models without alignment1 between input data and labels.
CTC was proposed by Juergen Schmidhuber's group at The Swiss AI Lab IDSIA (Istituto Dalle Molle di Studi sull'Intelligenza Artificiale) in 2006[1].
CTC is computationally expensive.
warp-CTC is a fast paralleled implementation of CTC on GPU and CPU to save the time for calculating the output of CTC.
warp-CTC model can recognize the speeches of two vastly different languages namely English and Chinese.
warp-CTC was proposed by Baidu Research – Silicon Valley AI Lab in 2015 and open-sourced the code of warp-CTC in 2016[2,6].
CTC
CTC model can be defined as
p(Y|X)
X=x1,x2,...xT (X can be audio or processed spectrogram)
Y=y1,y2,....yL (Y can be a text sequence, y ∈{a,b,c,d,...z,?..!...<b>}. <b> is the token representing blank)
T>=L
Fig1[4].
For the case of speech recognition as fig. 1, X and Y are the input audio spectrogram of the speech and the output transcript sequence respectively. The length of the input sequence T can be equal or longer than the output sequence L.
How CTC deals with the unaligned input data and labels
The token <b> represents blank in Y
Consider the following output Y1 to Y3
Y1=(ccc<b>aa<b>t<b>)
Y2=(c<b><b>aa<b>t)
Y3=(<b>c<b>a<b>t)
Y1,Y2 and Y3 can be mapped to the same target transcript cat.
The duplication of the tokens in Y represent the all possible paths of generating the target transcript cat.
Fig2[4].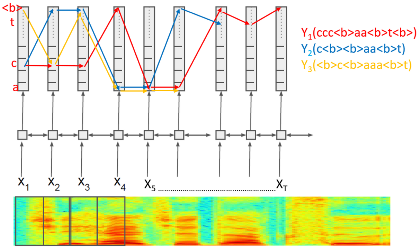
Fig2 describes the generation of 3 possible paths of target transcript cat.
Doing softmax at time t gives a probability of observing label k at time t i.e p(k,t|X).
Taking Y1=(ccc<b>aa<b>t<b>)as example, at time t=1, input is x1 and label c gets the maximum probability of observing so y1 turns to be c. At time t=2, input is x2 and label c gets the maximum probability of observing so y2 turns to be c,too. At time t=4, input is x4 and label <b> gets the maximum probability of observing so y4 turns to be blank.
The log probability of observing label k at time t is log p(k,t|X). The log probability of any path is the sum of the log probability of individual label at different time t. The log probability of any target transcript is the sum of the log probability of all paths which correspond to the target transcript.
It is possible to compute both the log probability of p( target transcript |X) and the gradient of log p(target transcript |X).
Therefore back propagation works when training an RNN-based network with CTC loss function.
Adapting warp-CTC to recognize Chinese speech
warp-CTC model can be applied to recognize Chinese speech with 2 adaptions[2].
I. Modifying the output layer with the outputs about 6000 characters including the Roman alphabets
II. Using a character level language model in Chinese
Reference
Graves, Alex, et al. "Connectionist temporal classification: labelling unsegmented sequence data with recurrent neural networks."_Proceedings of the 23rd international conference on Machine learning. _ACM, 2006.
Amodei, Dario, et al. "Deep speech 2: End-to-end speech recognition in english and mandarin." International Conference on Machine Learning. 2016.
https://web.stanford.edu/class/cs224n/archive/WWW_1617/lectures/cs224n-2017-lecture12.pdf
1. Using standard loss functions such as mean square errors or log negative likelihood to train RNN models requires timing information to align the input audio signal and the corresponding phoneme labels[3]. The alignment between input data and corresponding phoneme labels is illustrated in the figure[5] below.↩